To perform world-class research and education, universities must strive towards gender balance among employees, from students to professors. Scientific data supports the idea that diverse teams perform better, but progress is extremely slow. However, in the United Kingdom, a pioneering gender certification program is successfully increasing female faculty retention and promotion, awareness of unconscious gender bias, and a more unbiased work environment. Is this the magic bullet?

Pernilla Wittung-Stafshede, Chalmers University of Technology, writes about the program and its potential.
Looking at the statistics, it is clear that there is a gender problem in academia. Even in a liberal country such as Sweden, where there is paid parental leave often shared by both parents, there is a shortage of female professors and women in other top positions. The average percentage of women among professors at Swedish universities is 25% and this number is increasing by 1%, or less, per year. This is true despite that the Swedish government, for many years now, has set goals for each university to reach higher percentages of women professors. However, because there is no incentive for following such directives or penalty for not doing so, little progress has been made. There are many reasons for gender imbalance at universities; explanations to ‘leaky pipelines’ and ‘glass ceilings’ include unconscious bias, systemic and cultural forces that favor men. Instead of discussing why this problem exists, I will here describe a solution that seems to work.
The Athena SWAN Charter evolved from work between the Athena Project and the Scientific Women’s Academic Network (SWAN), to advance the representation of women in science, technology, engineering, medicine, and mathematics. With the support of Equality Challenge Unit (ECU) and the UK Research Council, the Charter was officially launched in 2005. At the start, the program included a modest 10 allied institutions. Athena SWAN is an evaluation and accreditation program that is based on data gathering, analysis, and scientific evidence. Today, the Athena SWAN program has expanded dramatically and evaluations show it has promoted tremendous success in enhancing gender equity at universities and institutions in the UK.
Athena SWAN is governed by 10 principles that encourage institutions to ensure that women from diverse backgrounds become positioned to reach their full potential. Through bronze, silver, and gold awards that institutions apply for, the Charter recognizes excellence in employment practices that advance and promote the careers of women and gender minorities. After receiving a bronze award, institutions can work towards a silver award by demonstrating a record of activities and achievements towards improving gender equity (often over several years) and at the same time, individual departments are allowed to apply for department-level awards. The key point is that the awards need to be renewed every four years. Thus one has to follow up on action plans made; if not, the award is lost. Currently, in the UK; 97 institutions hold an Athena SWAN award (2 are gold), and 587 departments have obtained awards (of which ten are gold awards). Among similar award schemes in Europe, Athena SWAN is by far the largest and has undergone the most robust evaluation. Impact has been demonstrated through women’s perception of improvement in their career development, achieving top-level support, positive change in the work environment and cultural change.
Data gathering and analysis, through a lens of gender, are used as the basis for making concrete action plans for structural and cultural changes at each institution. Examples of Athena SWAN activities include improved mentoring and training in career planning for young female researchers, and active work to encourage females to apply for promotion. Greater openness in promotion and recruitment processes is encouraged, as is the measurement of quality, rather than quantity, in research output. There is also strong emphasis on family friendly practices, and on developing inclusive working practices and culture. Reports indicate that those departments that are most successful concentrate on activities and policies that benefit all, not just women. For higher level awards (silver and gold), planned actions must be not only measurable, but also innovative and aspirational.
The Chemistry Department at York University, UK, is one of the pioneers of the Athena SWAN accreditation and the department was the first to receive a gold award. The department has gone from 0% to 40% female faculty over 20 years. Professor Paul Walton, faculty in this department, was one of initiators of gender equity efforts and acting chair when the gold award was achieved. He argues that the Athena SWAN program is successful because it focuses on scientific evidence. He also points out that because of his department’s gender work, it is now both highly ranked and very attractive to top researchers. However, he adds, there is no quick fix – establishing gender equality takes time.
The world is starting to open its eyes to Athena SWAN and it nowadays has pilots ongoing in Ireland and Australia. In the United States, NSF and AAAS are joining forces to start an initiative, and pilot efforts are also discussed in Japan and India. Athena SWAN received a major boost in 2011, when it was announced that the UK’s National Institute for Health Research would only shortlist medical schools for Biomedical Research Centre (BRC) and Unit (BRU) funding if the associate academic school holds a Silver Athena SWAN award. This was followed by similar requirements for other funding schemes. Clearly, such moves by funding agencies act as a strong incentive to universities (and their scientists) to participate and be successful with Athena SWAN accreditation.
Taken together, this may not be a magic bullet, but definitely a step in the right direction. One does not even need to develop something new, one can simply follow (with modifications) how they already do it in the UK. However, there is a caveat, which I noticed during my efforts along these lines: the country’s government must make a formal agreement with the Athena SWAN Charter in the UK to get going, and this costs money and requires commitment at the highest level. Thus, a first step is to lobby for this program’s potential with our leaders.
References
Athena SWAN Charter
https://www.ecu.ac.uk/equality-charters/athena-swan/
Athena SWAN 10 principles
https://www.ecu.ac.uk/equality-charters/athena-swan/about-athena-swan/
Statistics Athena SWAN 2017
https://www.ecu.ac.uk/equality-charters/athena-swan/2017-statistics/
Impact of Athena SWAN
https://www.ecu.ac.uk/equality-charters/charter-marks-explained/impact-equality-charters/
https://www.timeshighereducation.com/news/athena-swan-success-brings-new-challenges
 Tumor recurrence is an inevitable problem in cancer biology as it varies unpredictably among patients. Surprisingly, our knowledge of tumor recurrence still comes from analyses of post-resistant tumors or single time-point measurements. Critical events during early response that precede resistance and the actual dynamics of drug response in cancer cells is still largely unexplored. The differential sensitivity of melanoma cells has remained puzzling. For instance, why would melanoma cells with the same oncogenic driver (i.e., BRAF-mutations) respond differently to targeted therapies?
Tumor recurrence is an inevitable problem in cancer biology as it varies unpredictably among patients. Surprisingly, our knowledge of tumor recurrence still comes from analyses of post-resistant tumors or single time-point measurements. Critical events during early response that precede resistance and the actual dynamics of drug response in cancer cells is still largely unexplored. The differential sensitivity of melanoma cells has remained puzzling. For instance, why would melanoma cells with the same oncogenic driver (i.e., BRAF-mutations) respond differently to targeted therapies?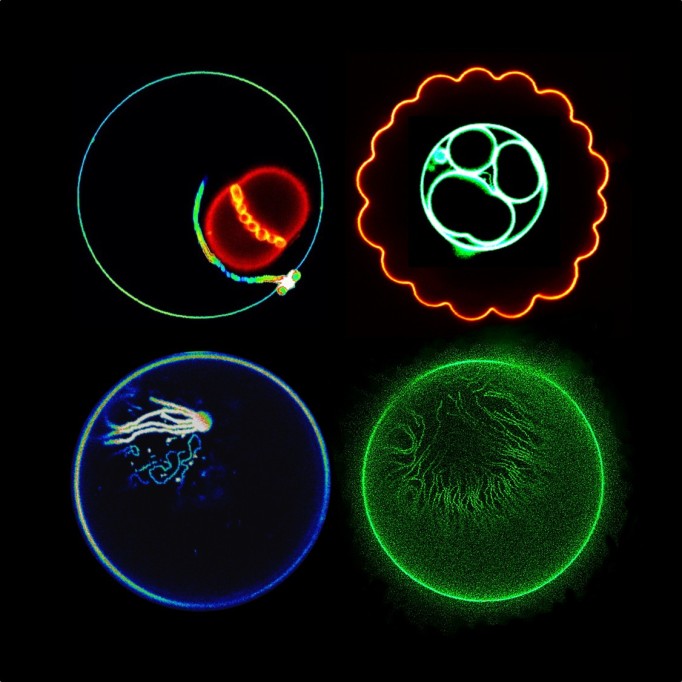




 When discussing biological lipid structures, the most commonly associated organizations are lamellar bilayers, liposomes, or micelles. Another organization is the bicontinuous cubic structure, where a lipid bilayer separates two water bodies tightly folded in three dimensions. A continuous unfolding between lamellar and apparent cubic-like organizations has been observed in the endoplasmatic reticulum of metazoan cells as well as the thylacoid membrane of chloroplasts. This behavior, along with their bicontinuous structure, has also made these structures an interesting target for drug delivery studies. Furthermore, continuous unfolding of cubic-like lipid structures has been proposed as a mechanism involved in the formation of the human skin barrier, which is situated in the top-most layer of the human skin, the stratum corneum. Utilizing coarse-grained molecular dynamics simulations, we set out to test the hypothesis that a deglycosylation of glycosylceramide headgroups, combined with dehydration of the lipid structure, could be important for the transformation of a cubic-like lipid structure into a lamellar bilayer structure.
When discussing biological lipid structures, the most commonly associated organizations are lamellar bilayers, liposomes, or micelles. Another organization is the bicontinuous cubic structure, where a lipid bilayer separates two water bodies tightly folded in three dimensions. A continuous unfolding between lamellar and apparent cubic-like organizations has been observed in the endoplasmatic reticulum of metazoan cells as well as the thylacoid membrane of chloroplasts. This behavior, along with their bicontinuous structure, has also made these structures an interesting target for drug delivery studies. Furthermore, continuous unfolding of cubic-like lipid structures has been proposed as a mechanism involved in the formation of the human skin barrier, which is situated in the top-most layer of the human skin, the stratum corneum. Utilizing coarse-grained molecular dynamics simulations, we set out to test the hypothesis that a deglycosylation of glycosylceramide headgroups, combined with dehydration of the lipid structure, could be important for the transformation of a cubic-like lipid structure into a lamellar bilayer structure.
 — Robin Thompson is a Junior Research Fellow at Christ Church, one of the constituent colleges of the University of Oxford. His research involves using mathematical models for forecasting during outbreaks of infectious disease in human, animal and plant populations. For more information about Dr Thompson or his most recent publications, or to collaborate with him on a project, see
— Robin Thompson is a Junior Research Fellow at Christ Church, one of the constituent colleges of the University of Oxford. His research involves using mathematical models for forecasting during outbreaks of infectious disease in human, animal and plant populations. For more information about Dr Thompson or his most recent publications, or to collaborate with him on a project, see  In honor of Biophysics Week and Brain Awareness Week, we asked Biophysical Society member Anna Koster, PhD student in the labs of
In honor of Biophysics Week and Brain Awareness Week, we asked Biophysical Society member Anna Koster, PhD student in the labs of 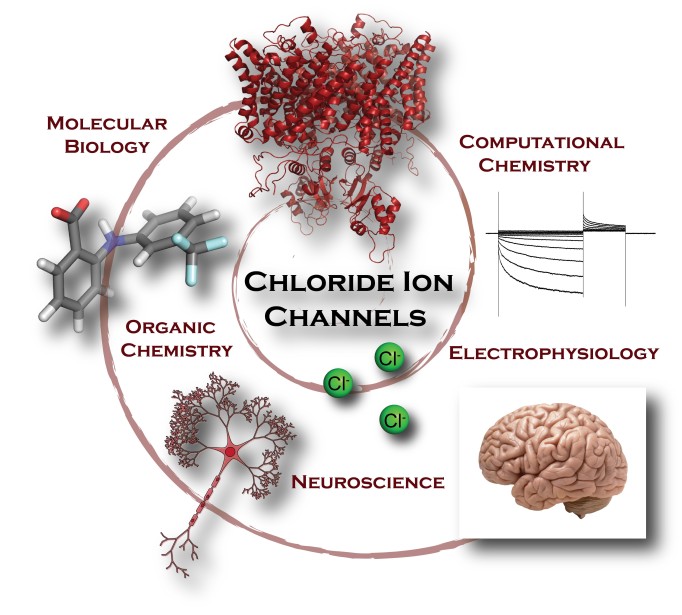
 Does the quaternary structure implied by crystal packing of a macromolecule exist in solution? Which one(s) of the variable loop positions suggested by NMR data exist? What conformations constitute the ensemble of structures in a solution of intrinsically disordered proteins or flexible nucleic acids? To answer these questions one requires a hydrodynamic model that connects the solution behavior to the structural coordinates.
Does the quaternary structure implied by crystal packing of a macromolecule exist in solution? Which one(s) of the variable loop positions suggested by NMR data exist? What conformations constitute the ensemble of structures in a solution of intrinsically disordered proteins or flexible nucleic acids? To answer these questions one requires a hydrodynamic model that connects the solution behavior to the structural coordinates. Daniel Beard
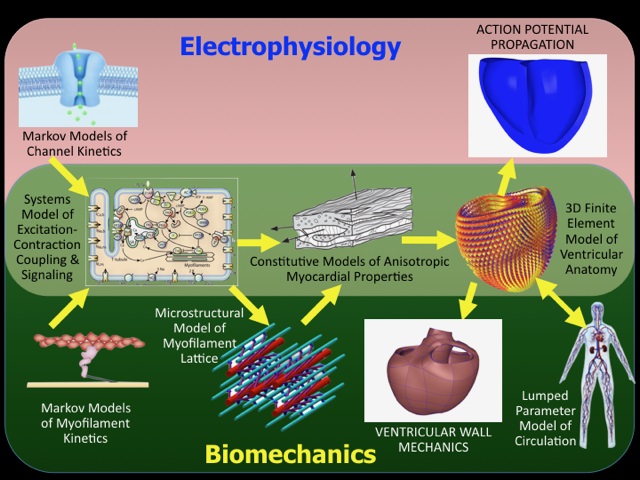
Daniel Beard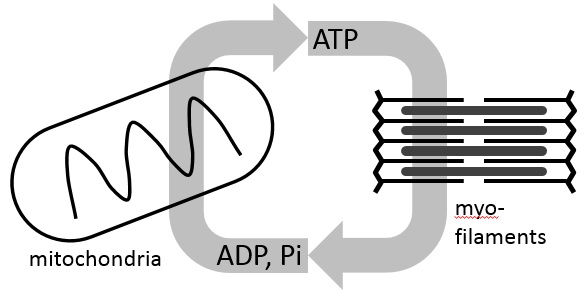
 Andrew McCulloch
Andrew McCulloch